路径规划与轨迹优化 —— A＊算法

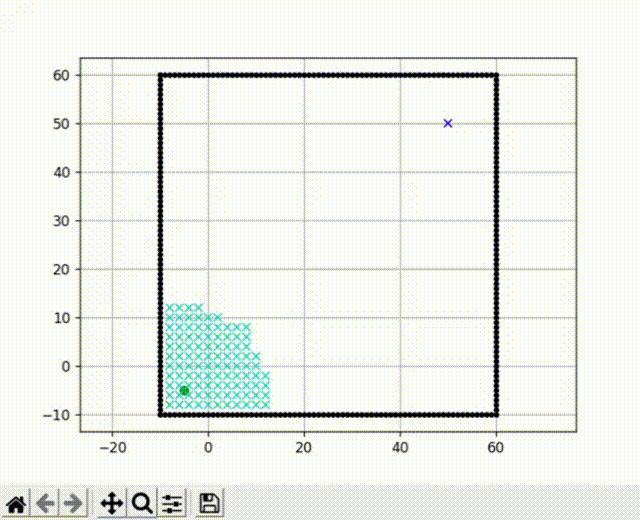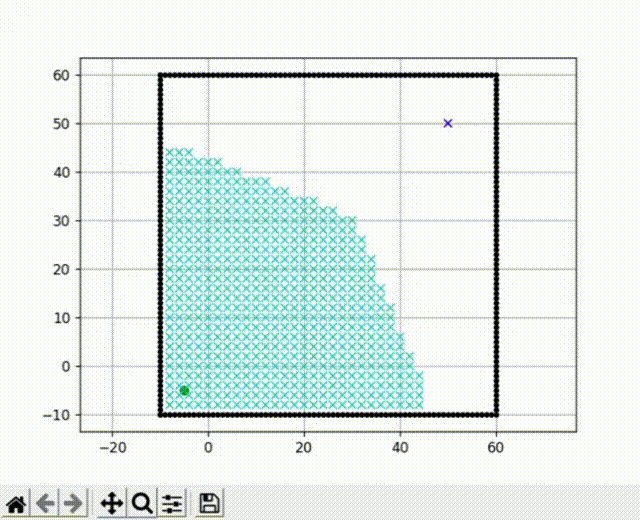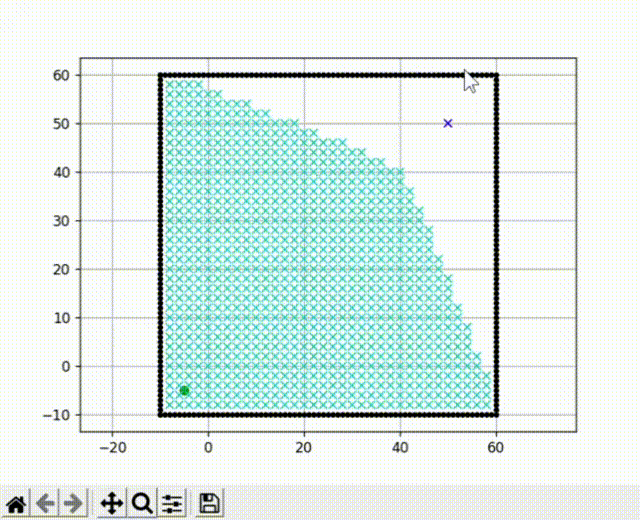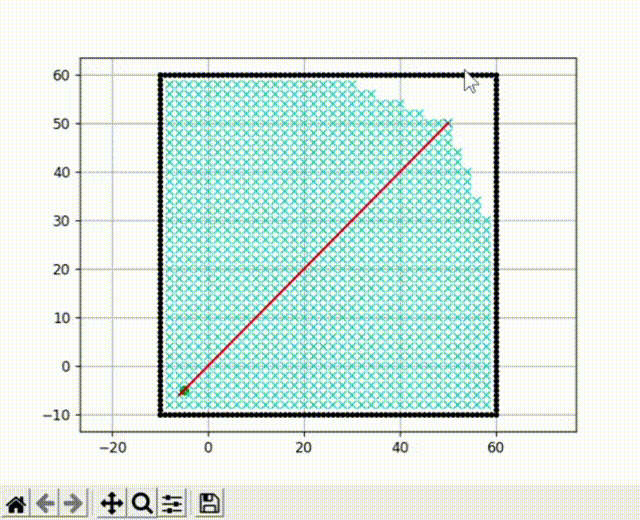
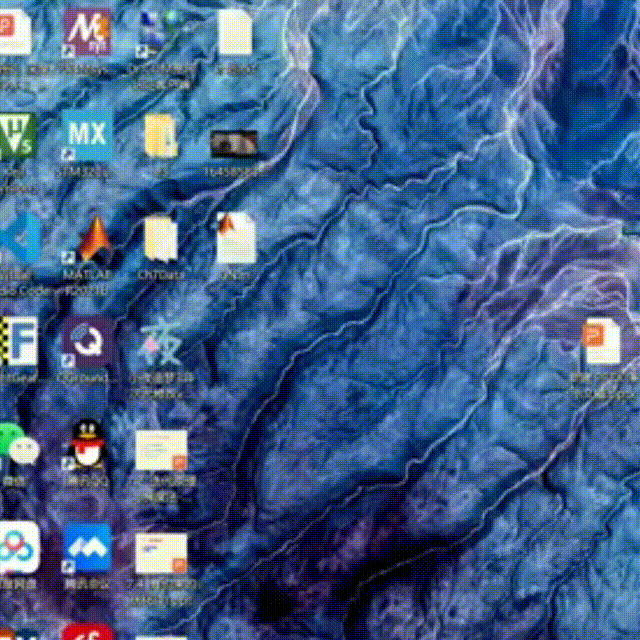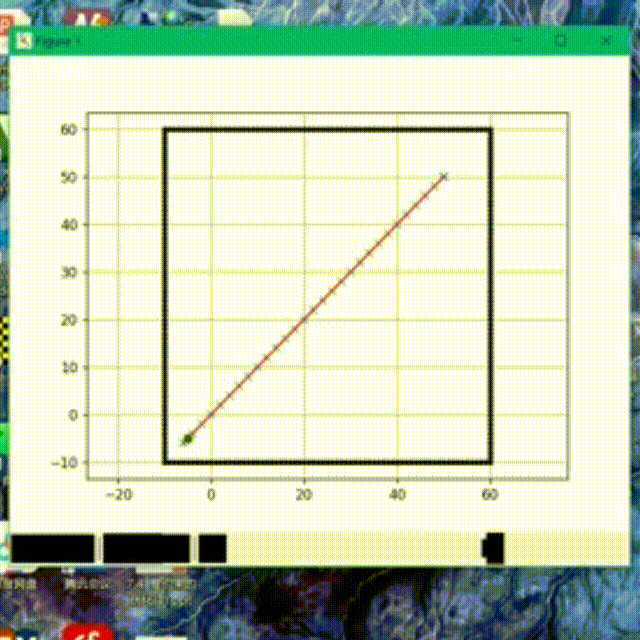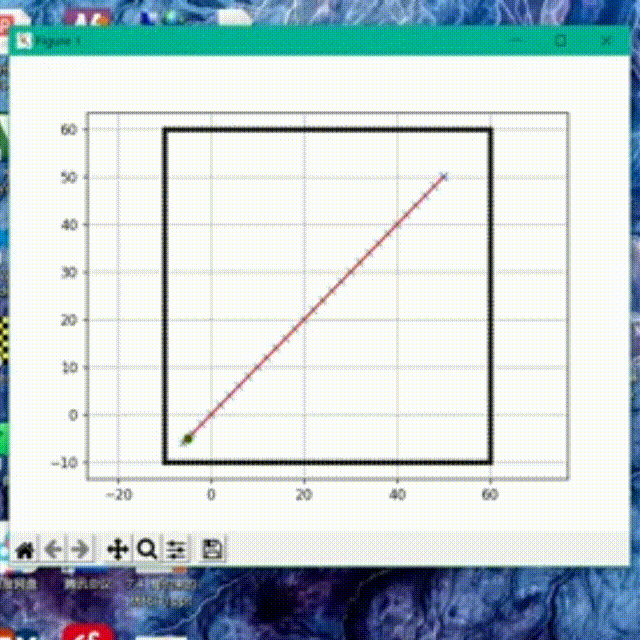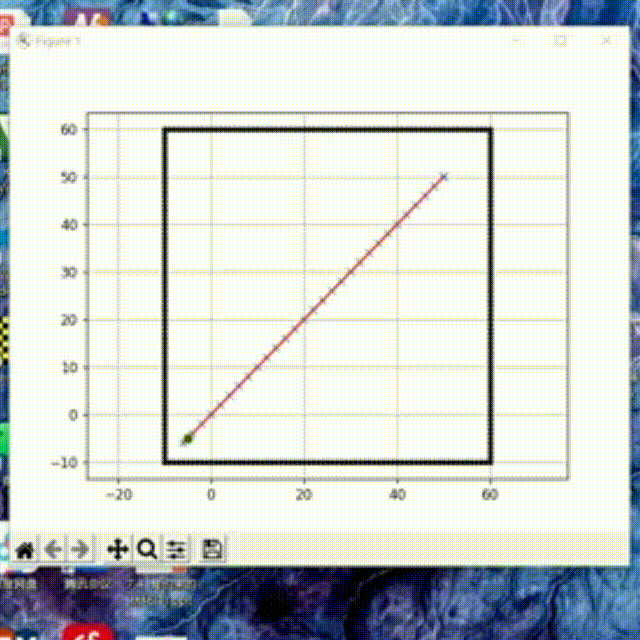
前面提到的Dijkstra算法是一种广度优先搜索算法，它以广度作为优先级，这种特性决定了它在搜索到终点前会尽可能大范围的遍历所有节点。我们运行前文的代码，可以看到广度优先搜索的效果有点像“病毒扩散”。

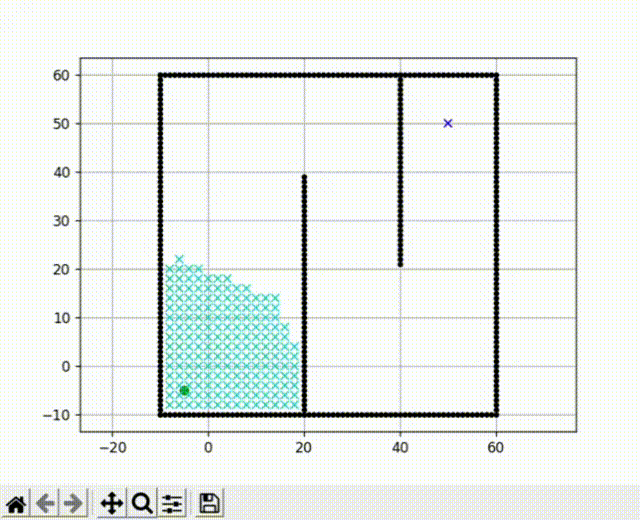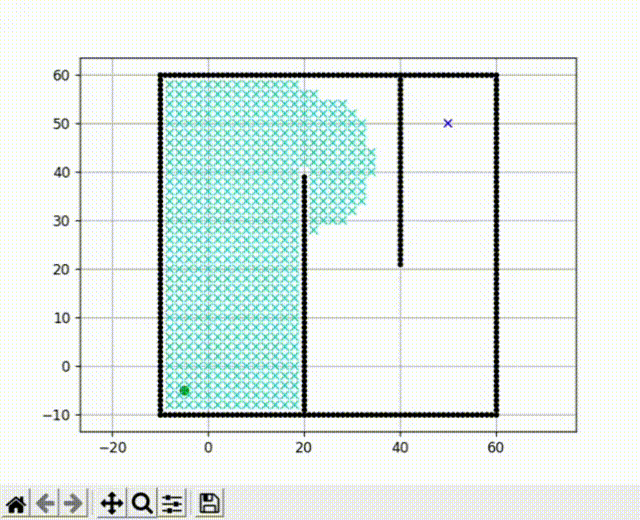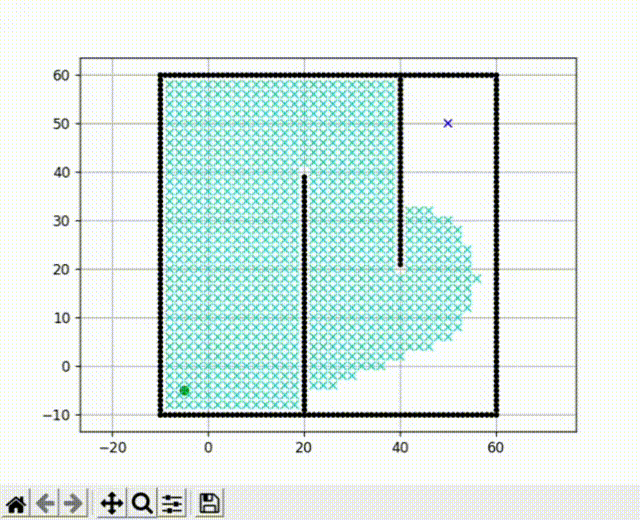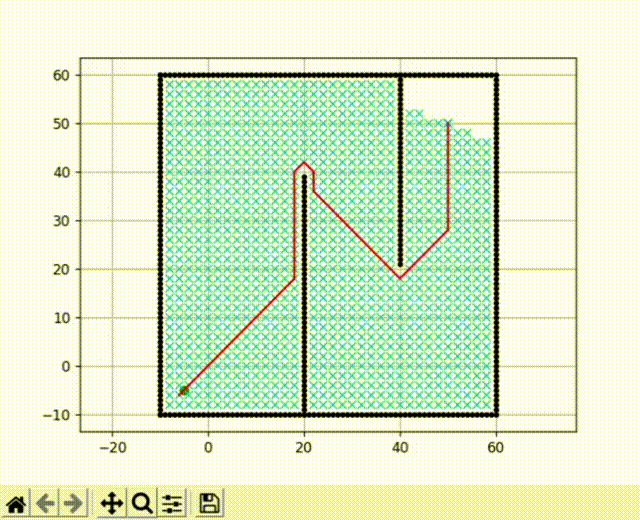
但在实际工程应用中，我们希望减少对节点的收录，并使机器人可以尽快的找到搜索方向。我们的思路是加入一个启发式函数来引导路径的规划。

$$f(n)=g(n)+h(n)$$
其中

• f(n)是节点n的综合优先级。当我们选择下一个要遍历的节点时，我们总会选取综合优先级最高（值最小）的节点。
• g(n) 是节点n距离起点的代价。
• h(n) 是节点n距离终点的代价，这也就是A*算法的启发函数。

加入启发式函数，可以形象的理解为终点的位置对规划产生了一个"引力"，促使着收录节点时更快的向终点进发。所以起点和终点都在影响着A*算法的行为

• 当启发函数h(n)始终为0，则将由g(n)决定节点的优先级，此时算法就变成了Dijkstra算法。
• 如果h(n)始终小于等于节点n到终点的代价，则A*算法保证一定能够找到最短路径。但是当h(n)的值越小，算法将遍历越多的节点，也就导致算法越慢。
• 如果h(n)完全等于节点n到终点的代价，则A*算法将找到最佳路径，并且速度很快。可惜的是，并非所有场景下都能做到这一点。因为在没有达到终点之前，我们很难确切算出距离终点还有多远。
• 如果h(n)的值比节点n到终点的代价要大，则A*算法不能保证找到最短路径，不过此时会很快。

所以A*算法能找到最短路径，依然保证最优性的条件是

$$h(n)\le h(n{)}_{真实距离}$$

A*算法在算法流程上只比Dijkstra算法多加入了启发式函数，其余没有变化

补充一些关于地图距离的知识点。不同的地图影响着启发式函数的值。

曼哈顿距离

如果机器人的行走规则中只允许朝上下左右四个方向移动，则使用曼哈顿距离来衡量两个点之间的距离。

对角距离

如果机器人可以斜向行走，则使用对角距离。计算对角距离的函数如下

其中D2是斜向行走的代价，它的计算如下

$$D2=\sqrt{2}D$$

欧式距离

欧几里得距离是指两个节点之间的直线距离。计算函数如下

定义机器人的运动规则有上下左右和斜向方式

因此启发式函数的计算采用对角距离

完整代码如下：

我们将Dijkstra算法的运行结果和A* 算法的结果放在一起可以发现，Dijkstra找到的是最短距离，但收录了大量节点，搜索速度慢。而A* 算法收录节点少，搜索速度快，但并不是最短距离。

我们把障碍物去掉，单纯比较算法的搜索速度可以发现，A* 算法最快的找到了终点，而Dijkstra收录了大量的节点，速度明显不如A* 算法。